| The PANEL Procedure |
| Heteroscedasticity-Corrected Covariance Matrices |
The MODEL statement HCCME= option is used to select the type of heteroscedasticity- consistent covariance matrix. In the presence of heteroscedasticity, the covariance matrix has a complicated structure which can result in inefficiencies in the OLS estimates and biased estimates of the variance covariance matrix. Consider the simple linear model (this discussion parallels the discussion in Davidson and MacKinnon, 1993, pg. 548-562):
 |
The assumptions that make the linear regression best linear unbiased estimator (BLUE) are 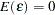 and
and 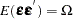 , where
, where 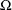 has the simple structure
has the simple structure  . Heteroscedasticity results in a general covariance structure, so that it is not possible to simplify
. Heteroscedasticity results in a general covariance structure, so that it is not possible to simplify 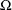 . The result is the following:
. The result is the following:
 |
As long as the following is true, then you are assured that the OLS estimate is consistent and unbiased:
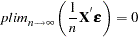 |
If the regressors are nonrandom, then it is possible to write the variance of the estimated  as the following:
as the following:
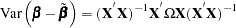 |
The effect of structure in the variance covariance matrix can be ameliorated by using generalized least squares (GLS), provided that 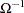 can be calculated. Using
can be calculated. Using 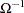 , you premultiply both sides of the regression equation,
, you premultiply both sides of the regression equation,
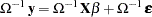 |
The resulting GLS  is
is
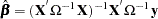 |
Using the GLS  , you can write
, you can write
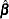 |
 |
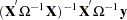 |
|||
 |
 |
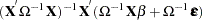 |
|||
 |
 |
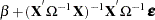 |
The resulting variance expression for the GLS estimator is
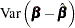 |
 |
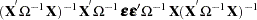 |
|||
 |
 |
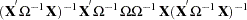 |
|||
 |
 |
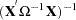 |
The difference in variance between the OLS estimator and the GLS estimator can be written as
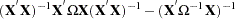 |
By the Gauss Markov Theory, the difference matrix must be positive definite under most circumstances (zero if OLS and GLS are the same, when the usual classical regression assumptions are met). Thus, OLS is not efficient under a general error structure. It is crucial to realize is that OLS does not produce biased results. It would suffice if you had a method for estimating a consistent covariance matrix and you used the OLS  . Estimation of the
. Estimation of the 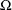 matrix is by no means simple. The matrix is square and has
matrix is by no means simple. The matrix is square and has  elements, so unless some sort of structure is assumed, it becomes an impossible problem to solve. However, the heteroscedasticity can have quite a general structure. White (1980) shows that it is not necessary to have a consistent estimate of
elements, so unless some sort of structure is assumed, it becomes an impossible problem to solve. However, the heteroscedasticity can have quite a general structure. White (1980) shows that it is not necessary to have a consistent estimate of 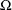 . On the contrary, it suffices to get an estimate of the middle expression. That is, you need an estimate of:
. On the contrary, it suffices to get an estimate of the middle expression. That is, you need an estimate of:
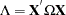 |
This matrix, 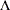 , is easier to estimate because its dimension is K. PROC PANEL provides the following classical HCCME estimators:
, is easier to estimate because its dimension is K. PROC PANEL provides the following classical HCCME estimators:
The matrix 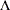 is approximated by:
is approximated by:
HCCME=N0: This is the simple OLS estimator so
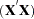 . If you do not request the HCCME= option, then PROC PANEL defaults to this estimator.
. If you do not request the HCCME= option, then PROC PANEL defaults to this estimator. HCCME=0:

The
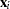 constitutes the
constitutes the 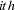 row of the matrix
row of the matrix  .
. HCCME=1:

HCCME=2:

The
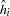 term is
term is  th diagonal element of the so called hat matrix. The expression for
th diagonal element of the so called hat matrix. The expression for 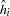 is
is  . The hat matrix attempts to adjust the estimates for the presence of influence or leverage points.
. The hat matrix attempts to adjust the estimates for the presence of influence or leverage points. HCCME=3:
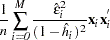
HCCME=4: This is the Arellano (1987) version of the White (1980) HCCME for panel. PROC PANEL includes an option for the calculation of the Arellano (1987) version of the White HCCME in the panel setting. Arellano’s insight is that in a panel there are
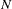 covariance matrices, each corresponding to a cross section. Forming the White (1980) HCCME for each panel, you need to take only the average of those
covariance matrices, each corresponding to a cross section. Forming the White (1980) HCCME for each panel, you need to take only the average of those 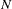 estimators that yield Arellano. The details of the estimation follow. First, you arrange the data such that the first cross section occupies the first
estimators that yield Arellano. The details of the estimation follow. First, you arrange the data such that the first cross section occupies the first 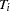 observations. You treat the panels as separate regressions with the form:
observations. You treat the panels as separate regressions with the form: 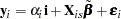
The parameter estimates
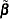 and
and 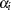 are the result of LSDV or within estimator.
are the result of LSDV or within estimator.  is a vector ones of length
is a vector ones of length 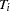 . The estimate of the
. The estimate of the  th cross section’s
th cross section’s 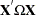 matrix (where the
matrix (where the  subscript indicates that no constant column has been suppressed to avoid confusion) is
subscript indicates that no constant column has been suppressed to avoid confusion) is 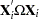 . The estimate for the whole sample is:
. The estimate for the whole sample is: 
The Arellano standard error is in fact a White-Newey-West estimator with constant and equal weight on each component. It should be noted that, in the between estimators, selecting HCCME = 4 returns the HCCME = 0 result since there is no 'other' variable to group by.
In their discussion, Davidson and MacKinnon (1993, pg. 554) argue that HCCME=1 should always be preferred to HCCME=0. While generally HCCME=3 is preferred to 2 and 2 is preferred to 1, the calculation of HCCME=1 is as simple as the calculation of HCCME=0. Therefore, it is clear that HCCME=1 is preferred when the calculation of the hat matrix is too tedious.
All HCCME estimators have well defined asymptotic properties. The small sample properties are not well known, and care must exercised when sample sizes are small.
The HCCME estimator of 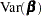 is used to drive the covariance matrices for the fixed effects and the Lagrange multiplier standard errors. Robust estimates of the variance covariance matrix for
is used to drive the covariance matrices for the fixed effects and the Lagrange multiplier standard errors. Robust estimates of the variance covariance matrix for  imply robust variance covariance matrices for all other parameters.
imply robust variance covariance matrices for all other parameters.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.