| The PANEL Procedure |
| Parks Method (Autoregressive Model) |
Parks (1967) considered the first-order autoregressive model in which the random errors 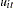 ,
,  , and
, and 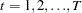 have the structure
have the structure
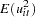 |
 |
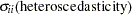 |
|||
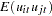 |
 |
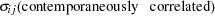 |
|||
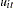 |
 |
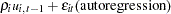 |
where
 |
 |
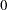 |
|||
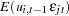 |
 |
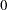 |
|||
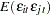 |
 |
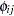 |
|||
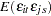 |
 |
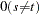 |
|||
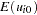 |
 |
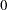 |
|||
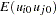 |
 |
 |
The model assumed is first-order autoregressive with contemporaneous correlation between cross sections. In this model, the covariance matrix for the vector of random errors u can be expressed as
 |
where
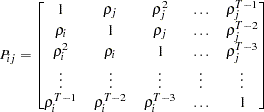 |
The matrix V is estimated by a two-stage procedure, and 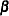 is then estimated by generalized least squares. The first step in estimating V involves the use of ordinary least squares to estimate
is then estimated by generalized least squares. The first step in estimating V involves the use of ordinary least squares to estimate 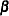 and obtain the fitted residuals, as follows:
and obtain the fitted residuals, as follows:
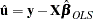 |
A consistent estimator of the first-order autoregressive parameter is then obtained in the usual manner, as follows:
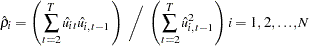 |
Finally, the autoregressive characteristic of the data is removed (asymptotically) by the usual transformation of taking weighted differences. That is, for 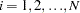 ,
,
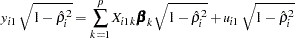 |
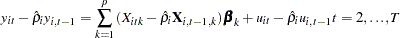 |
which is written
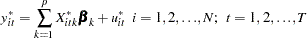 |
Notice that the transformed model has not lost any observations (Seely and Zyskind 1971).
The second step in estimating the covariance matrix V is applying ordinary least squares to the preceding transformed model, obtaining
 |
from which the consistent estimator of 
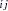 is calculated as follows:
is calculated as follows:
 |
where
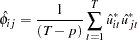 |
Estimated generalized least squares (EGLS) then proceeds in the usual manner,
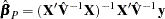 |
where 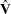 is the derived consistent estimator of V. For computational purposes,
is the derived consistent estimator of V. For computational purposes, 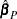 is obtained directly from the transformed model,
is obtained directly from the transformed model,
 |
where  .
.
The preceding procedure is equivalent to Zellner’s two-stage methodology applied to the transformed model (Zellner 1962).
Parks demonstrates that this estimator is consistent and asymptotically, normally distributed with
 |
Standard Corrections
For the PARKS option, the first-order autocorrelation coefficient must be estimated for each cross section. Let 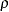 be the
be the 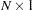 vector of true parameters and
vector of true parameters and 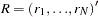 be the corresponding vector of estimates. Then, to ensure that only range-preserving estimates are used in PROC PANEL, the following modification for R is made:
be the corresponding vector of estimates. Then, to ensure that only range-preserving estimates are used in PROC PANEL, the following modification for R is made:
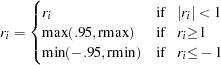 |
where
 |
and
 |
Whenever this correction is made, a warning message is printed.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.