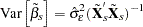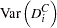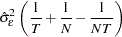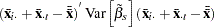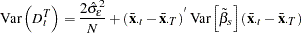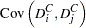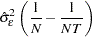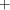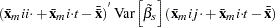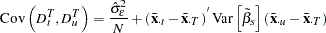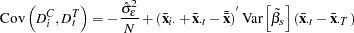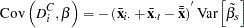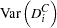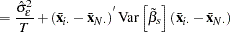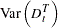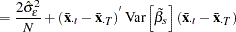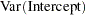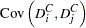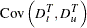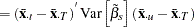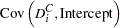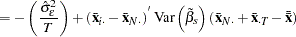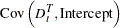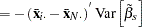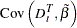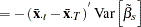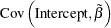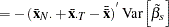Assume that the data are balanced (for example, all cross sections have T observations). Then you can write the following:
where the symbols:
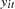 and
and 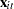 are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables not including a constant), respectively
are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables not including a constant), respectively
 and
and 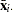 are cross section means
are cross section means
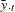 and
and 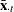 are time means
are time means
 and
and 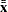 are the overall means
are the overall means
The two-way fixed-effects model is simply a regression of 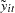 on
on 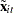 . Therefore, the two-way
. Therefore, the two-way  is given by:
is given by:
The calculations of cross section dummy variables, time dummy variables, and intercepts follow in a fashion similar to that used in the one-way model.
First, you obtain the net cross-sectional and time effects. Denote the cross-sectional effects by 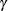 and the time effects by
and the time effects by  . These effects are calculated from the following relations:
. These effects are calculated from the following relations:
Denote the cross-sectional dummy variables and time dummy variables with the superscript C and T. Under the NOINT option the following equations give the dummy variables:
When an intercept is specified, the equations for dummy variables and intercept are:
The sum of squared errors is:
The estimated error variance is:
With or without a constant, the variance covariance matrix of  is given by:
is given by:
Variance Covariance of Dummy variables with No Intercept
The variances and covariances of the dummy variables are given with the NOINT specification as follows:
Variance Covariance of Dummy variables with Intercept
The variances and covariances of the dummy variables are given when the intercept is included as follows:
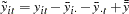
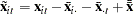
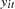 and
and 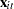 are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables not including a constant), respectively
are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables not including a constant), respectively  and
and 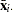 are cross section means
are cross section means 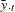 and
and 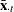 are time means
are time means  and
and 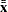 are the overall means
are the overall means 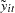 on
on 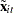 . Therefore, the two-way
. Therefore, the two-way  is given by:
is given by: 
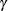 and the time effects by
and the time effects by  . These effects are calculated from the following relations:
. These effects are calculated from the following relations: 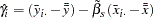
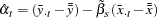
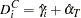
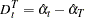

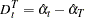
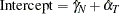
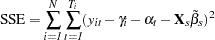
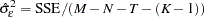
 is given by:
is given by: