The multinomial probit model allows the random components of the utility of the different alternatives to be nonindependent and nonidentical. Thus, it does not have the IIA property. The increase in the flexibility of the error structure comes at the expense of introducing several additional parameters in the covariance matrix of the errors.

Consider the random utility function

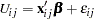where the joint distribution of 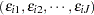is multivariate normal:

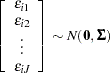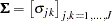The dimension of the error covariance matrix is determined by the number of alternatives . Given 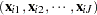, the th 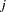alternative is chosen if and only if 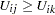for all . Thus, the probability that the 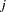th alternative is chosen is

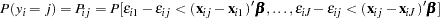where 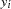is a random variable that indicates the choice made. This is a cumulative probability from a -variate normal distribution. Since evaluation of this probability involves multidimensional integration, it is practical to use a simulation method to estimate the model. Many studies have shown that the simulators proposed by Geweke (1989), Hajivassiliou (1993), and Keane (1994) (GHK) perform well. For example, Hajivassiliou, McFadden, and Ruud (1996) compare 13 simulators using 11 different simulation methods and conclude that the GHK simulation method is the most reliable. To compute the probability of the multivariate normal distribution, the recursive simulation method is used. Refer to Hajivassiliou (1993) for more details on GHK simulators.

The log-likelihood function for the multinomial probit model can be written as

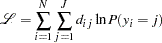where

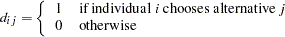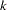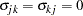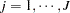For identification of the multinomial probit model, two of the diagonal elements of are normalized to 1, and it is assumed that for one of the choices whose error variance is normalized to 1 (say, ), it is also true that for and 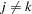. Thus, a model with alternatives has at most 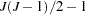covariance parameters after normalization.

Let 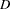and 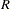be defined as

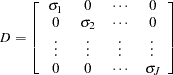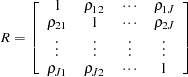where 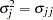and 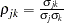. Then, for identification, and 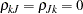, for all 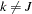can be imposed, and the error covariance matrix is .

In the standard MDC output, the parameter estimates STD_j and RHO_jk correspond to 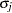and .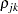

In principle, the multinomial probit model is fully identified with the preceding normalizations. However, in practice, convergence in applications of the model with more than three alternatives often requires additional restrictions on the elements of .

It must also be noted that the unrestricted structure of the error covariance matrix makes it impossible to forecast demand for a new alternative without knowledge of the new by error covariance matrix.