| The MDC Procedure |
| Heteroscedastic Extreme-Value Model |
The heteroscedastic extreme-value (HEV) model (Bhat 1995) allows the random components of the utility function to be nonidentical. Specifically, the HEV model assumes independent but nonidentical error terms distributed with the type I extreme-value distribution. The HEV model allows the variances of the random components of utility to differ across alternatives. Bhat (1995) argues that the HEV model does not have the IIA property. The HEV model contains the conditional logit model as a special case. The probability that an individual  will choose alternative
will choose alternative 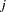 from the set
from the set 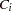 of available alternatives is
of available alternatives is
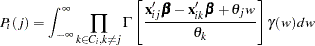 |
where the choice set 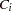 has
has 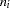 elements and
elements and
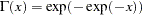 |
 |
are the cumulative distribution function and probability density function of the type I extreme-value distribution. The variance of the error term for the 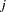 th alternative is
th alternative is 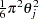 . If the scale parameters,
. If the scale parameters, 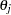 , of the random components of utility of all alternatives are equal, then this choice probability is the same as that of the conditional logit model. The log-likelihood function of the HEV model can be written as
, of the random components of utility of all alternatives are equal, then this choice probability is the same as that of the conditional logit model. The log-likelihood function of the HEV model can be written as
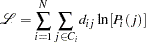 |
where
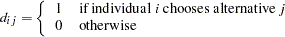 |
Since the log-likelihood function contains an improper integral function, it is computationally difficult to get a stable estimate. With the transformation 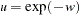 , the probability can be written
, the probability can be written
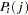 |
 |
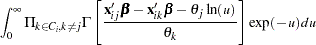 |
|||
 |
 |
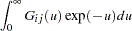 |
Using the Gauss-Laguerre weight function, 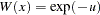 , the integration of the log-likelihood function can be replaced with a summation as follows:
, the integration of the log-likelihood function can be replaced with a summation as follows:
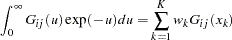 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.