| Introduction |
| Vector Time Series Analysis |
The VARMAX procedure enables you to model the dynamic relationship both between the dependent variables and between the dependent and independent variables. The VARMAX procedure includes the following features:
several modeling features:
vector autoregressive model
vector autoregressive model with exogenous variables
vector autoregressive and moving-average model
Bayesian vector autoregressive model
vector error correction model
Bayesian vector error correction model
GARCH-type multivariate conditional heteroscedasticity models
criteria for automatically determining AR and MA orders:
Akaike information criterion (AIC)
corrected AIC (AICC)
Hannan-Quinn (HQ) criterion
final prediction error (FPE)
Schwarz Bayesian criterion (SBC), also known as Bayesian information criterion (BIC)
AR order identification aids:
partial cross-correlations
Yule-Walker estimates
partial autoregressive coefficients
partial canonical correlations
testing the presence of unit roots and cointegration:
Dickey-Fuller tests
Johansen cointegration test for nonstationary vector processes of integrated order one
Stock-Watson common trends test for the possibility of cointegration among nonstationary vector processes of integrated order one
Johansen cointegration test for nonstationary vector processes of integrated order two
model parameter estimation methods:
least squares (LS)
maximum likelihood (ML)
model checks and residual analysis using the following tests:
Durbin-Watson (DW) statistics
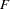 test for autoregressive conditional heteroscedastic (ARCH) disturbance
test for autoregressive conditional heteroscedastic (ARCH) disturbance 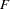 test for AR disturbance
test for AR disturbance Jarque-Bera normality test
Portmanteau test
seasonal deterministic terms
subset models
multiple regression with distributed lags
dead-start model that does not have present values of the exogenous variables
Granger-causal relationships between two distinct groups of variables
infinite order AR representation
impulse response function (or infinite order MA representation)
decomposition of the predicted error covariances
roots of the characteristic functions for both the AR and MA parts to evaluate the proximity of the roots to the unit circle
contemporaneous relationships among the components of the vector time series
forecasts
conditional covariances for GARCH models
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.