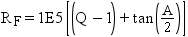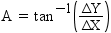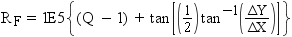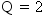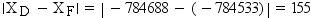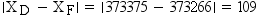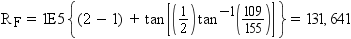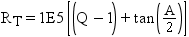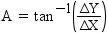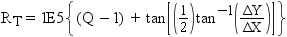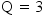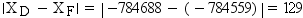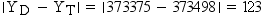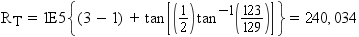Chain Rank Calculation Examples

Calculating Chain Rank

Overview

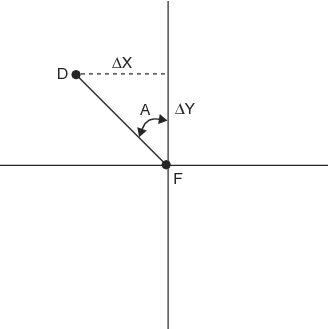
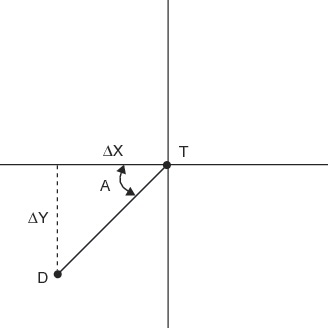
The from-node and to-node rank values are expressed as a single number in the form ffffff.tttttt. Therefore, the rank for the chain in Example: Calculating From-Node Rank and Example: Calculating To-Node Rank is 131641.240034. This is the value of the RANK variable for this chain in the chains data set.
Note: The trigonometric functions for calculating the RANK value in the following sections are in radians.

Point Coordinates

The information in the following table is used in the following examples:
Coordinate Values for a Chain with One Detail Point
Point
Description
X
Y
F
From-node of chain
-784533
373266
D
Detail point
-784688
373375
T
To-node of chain
-784559
373498

Variable Definitions

The variables used in the equations have the following definitions:
RF
is the rank value at the from-node of the chain.
RT
is the rank value at the to-node of the chain.
A
is the angle from the chain clockwise to the nearest X or Y axis.
ΔX
is the length of a chain segment along the X axis.
ΔY
is the length of a chain segment along the Y axis.

Example: Calculating From-Node Rank

The following equations illustrate the steps necessary to calculate the from-node rank:
Given
The From-Node RANK value equals the one E five multiplier transform of Q minus one plus the tangent of A divided by two
and
A equals the tangent to the power of negative one of delta Y divided by delta X
then
The From-Node RANK value equals the one E five multiplier transform of Q minus one plus the tangent of one half of the tangent to the power of negative one of delta Y divided by delta X
The following example illustrates calculating a from-node rank with the given values:
Given
Q equals two
and
the absolute value of X subscript D minus X subscript F equals the absolute value of negative seven hundred eighty four thousand six hundred eighty eight minus negative seven hundred eighty four thousand five hundred thirty three, which is one hundred fifty five
and
the absolute value of X subscript D minus X subscript F equals the absolute value of three hundred seventy three thousand three hundred seventy five minus three hundred seventy three thousand two hundred sixty six, which is one hundred and nine
then
The From-Node RANK value equals the one E five multiplier transform of two minus one plus the tangent of one half of the tangent to the power of negative one of one hundred and nine divided by one hundred fifty five, which is one hundred thirty one thousand six hundred forty one
Calculating the From-Node Rank
Calculating the From-Node Rank

Example: Calculating To-Node Rank

The following equations illustrate the steps necessary to calculate the to-node rank:
Given
The To-Node RANK value equals the one E five multiplier transform of Q minus one plus the tangent of A divided by two
and
A equals the tangent to the power of negative one of delta Y divided by delta X
then
The From-Node RANK value equals the one E five multiplier transform of Q minus one plus the tangent of one half of the tangent to the power of negative one of delta Y divided by delta X
The following example illustrates calculating a to-node rank with the given values:
Given
Q equals three
and
the absolute value of X subscript D minus X subscript F equals the absolute value of negative seven hundred eighty four thousand six hundred eighty eight minus negative seven hundred eighty four thousand five hundred fifty nine, which is one hundred twenty nine
and
the absolute value of Y subscript D minus Y subscript T equals the absolute value of three hundred seventy three thousand three hundred seventy five minus three hundred seventy three thousand four hundred ninety eight, which is one hundred twenty three
then
The To-Node RANK value equals the one E five multiplier transform of three minus one plus the tangent of one half of the tangent to the power of negative one of one hundred twenty three divided by one hundred twenty nine, which is two hundred forty thousand thirty four
Calculating the To-Node Rank
Calculating the To-Node Rank
Copyright © SAS Institute Inc. All rights reserved.