Glossary of ADX Terms: Glossary of ADX Terms :: Getting Started with the SAS(R) 9.2 ADX Interface for Design of Experiments

Glossary of ADX Terms

Alias Structure of a Design

In a fractional factorial design, it is impossible to completely distinguish the influences that all the effects have on the response. The aliasing structure of the design shows which effects are indistinguishable. Each row of the alias structure corresponds to a measurable effect on the response; any or all of the effects in a given row could be responsible for the measured effect. ADX provides a tab for examining the alias structure in the Design Details window.

See also Resolution. For details, refer to Montgomery (1997) or other standard references on design of experiments.

Analysis of Variance

Performing an analysis of variance (ANOVA) on a linear model enables you to assess the model effects on the variation in the response. The overall ANOVA analyzes the significance of the entire model.

Bayes Effect Plot

A Bayes effect plot displays the probability that each effect is active according to the Bayesian analysis of Box and Meyer (1986). This analysis is especially useful in saturated or near-saturated fractional factorial designs, when there are not enough degrees of freedom left to estimate error and perform 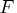tests on the effects. In this case, the principle of effect sparsity suggests that most of the effects in the design (about 80%) will be inactive.

With 0.20 as a prior probability for effect activity, posterior probabilities can be computed using standard Bayesian theory. Roughly speaking, this analysis gives the probability that each effect is active. The posterior probabilities can be quite sensitive to the prior. For this reason, you should examine the posteriors over a range of priors. If an effect has a high probability of activity over most of the range, this can be taken as good evidence that it indeed has a significant effect on the response.

Blocking Factor

A blocking factor is an experimental factor that might contribute to response variability but that is otherwise not of interest. Typically, a blocking factor can be controlled in laboratory conditions but not in field settings.

A blocking scheme is used in a factorial design to account for variability in the response that might otherwise be attributed incorrectly to other factors or to experimental error.

Box-Behnken Design

A Box-Behnken design is a fraction of a 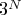design used to estimate a full quadratic model in 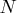factors. It consists of all 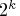possible combinations of high and low levels for different subsets of the factors of size 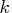, with all other factors at their central levels. The subsets are chosen according to a balanced incomplete block design for 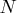treatments in blocks of size 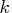. A number of center points with all factors at their central levels can also be added.

Since each factor takes no more than three different values, and since only 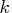factors are not at their central levels in any one run, these designs can be easier to implement than comparable central composite designs. However, unlike central composite designs, they are not conducive to sequential experimentation.

Box Plot

A box plot displays differences in the distributions of the selected response when categorized by factor levels. Like a main-effects plot, a box plot can demonstrate potentially significant effects. However, box plots can also bring to light the heteroscedasticity of the response (a significant effect of a factor on the variance of the response). ADX provides box plots with summary statistics such as the median and the interquartile range.

ADX can categorize the responses by using more than one factor; in this case the factors are stratified. This enables you to see the interaction of two effects on the mean and variance of the response, if enough data are present.

Center Point

Often the low and high values of a factor in a fractional factorial design are chosen around a central, nominal value---perhaps the current operating conditions. Center points are included in a design to add extra prediction precision in this region or to allow testing for lack of fit. You can add as many center points to the design as you want, although they are allowed only when at least one of the factors is numeric.

Central Composite Design

A central composite design for 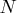factors is a full or fractional replication of the complete 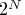design, augmented by 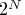axial points and a given number of center points. There is one axial point for either extreme of each factor, with all other factors at their central values. A center point has every factor at its central value. All terms in the second-order model can be estimated, and the center points enable you to test for a lack of fit.

Confounding Rules

The confounding rules for a fractional factorial design are the equations that specify how it is constructed. In general, for two-level factors, the confounding rules assign the values of certain factors to be the product of values of other factors. ADX chooses confounding rules that generate a maximum resolution design with minimum aberration.

Constrained Mixture Design

In a mixture design, when the mixture factors are subject to additional constraints (besides summing to one), there are two different possibilities for design generation:

If the constraints are lower bounds, then a regular simplex-centroid design can be transformed into a design for the constrained factors.
If there are both upper and lower bounds on the factors, then the feasible region no longer has a regular shape. However, the vertices and generalized face centroids of the feasible region provide good potential design points. ADX chooses an optimal design from these points when generating a constrained mixture design. Refer to Snee (1975) and Cornell (1990) for details.

Constraint

Sometimes the nature of an experiment does not allow you to set factor levels freely. These constraints are modeled through linear inequalities, such as

$x1 + x2 + x3 \le 0.8$

Constraints on the factors usually do not admit classical fractional factorial designs or response surface designs. ADX automatically uses an optimal design in these cases.

Mixture designs involving constraints often arise in practice. ADX uses a Scheffé analysis for these designs. See Constrained Mixture Design for more details.

Contour Optimizer

Resembling the contour plot in many ways, the contour optimizer in ADX gives a two-dimensional representation of a response surface. This tool is used to locate optimum factor settings for a desired response. The display can be annotated and included in a report. See Contour Plots for more details.

Contour Plot

A contour plot is a two-dimensional representation of a three-dimensional response surface, where curves of equal predicted response are plotted. If no more than two factors in the design appear to affect the response, the contour plot can be a good way to summarize the response surface. Otherwise, ADX provides a matrix of contour plots created by fixing levels of nondisplayed variables.

The contours of the standard error of prediction are printed along with those of the predicted response. This indicates how well the fitted response surface predicts the true response.

Cube Plot

A cube plot is a three-dimensional representation of the observed response surface, with the average responses indicated at the cube vertices. It is especially useful for fractional factorial designs when few factors and interactions are significant.

Design Augmentation

Sometimes a researcher needs more information from an experiment than is provided by an initial design. Through the addition of carefully chosen runs, the estimation and prediction capability can be enhanced. This process is called design augmentation.

ADX currently supports four types of design augmentation:

Augment a two-level design to a response surface design. This enables you to estimate quadratic effects. Center points and axial runs are added to the original design to make it a central composite design.
Fold over a two-level design. This involves adding complementary runs to a two-level fractional factorial design with Resolution 3. This increases the resolution to four but doubles the number of runs.
Break alias strings of certain effects by adding optimal runs. This technique, like folding over, allows the estimation of more effects but typically does not require the addition of as many runs. ADX uses the Optimal Design interface to generate these runs.
Deleting inactive factors and projecting into a higher-resolution design. This involves dropping the inactive factors permanently from an experiment and projecting the design in the subset of the remaining factors.

Design Type

ADX provides the following design types:

Two-Level Designs
Response Surface Designs
Mixture Designs
Mixed-Level Designs
Optimal Designs
Split-Plot Designs

Desirability

When an experiment involves multiple responses, the overall response outcome depends on all or some of the individual responses. For example, you might want to minimize the first response, maximize the second response, or keep the third response close to a target value. You can use the desirability feature available in the Prediction Profiler plot in the Optimize window to define a desirability function for each individual response. The overall desirability of the product would be the geometric mean of the desirability of individual responses. For more information, refer to Derringer and Suich (1980).

Factor

Also referred to as an independent or predictor variable, a factor is a variable included in a model to account for variation in a response. Factors are the variables whose values (levels) you set to study their relationship to a response. You often experiment with many potentially influential factors at the same time. However, the more factors there are in the experiment, the more runs will be required. Weigh the number of factors against the size and resolution of corresponding designs in order to determine which designs are appropriate for your situation.

Factorial Plot

A factorial plot shows a tree plot displaying the response for combinations of levels of the main effects. Each node represents the response for the associated combination of factor levels. Refer to Beckman (1996) for details.

Fractional Factorial Design

A fractional factorial design is a factorial design in which not all combinations of factor levels are run. These designs are useful when runs are costly and higher-order interactions are not significant.

Half-Normal Plot

A half-normal plot is a plot of the absolute values of the responses against the expected order statistics from a folded normal distribution. Outliers, which deviate from the standard deviation line, indicate possibly active effects.

Hybrid Design

Roquemore (1976) developed a set of saturated or near-saturated second-order designs called hybrid designs. A hybrid design is very efficient. Unlike the small composite designs, hybrid designs are quite competitive with central composite designs when design size is taken into account.

Influential Observation

An influential observation is an observation that has a large impact on the results. Note that these are different from outliers, which are observations not explained by the model. Influential observations should be analyzed with care.

Interaction Effect

An interaction effect measures the extent to which the effect of one factor on the response changes for different values of one or more other factors.

The presence of a factor in a significant interaction does not necessarily mean that its main effect is also significant. However, if an interaction is deemed to be significant and is therefore retained in the predictive model, it is good practice to include the constituent main effects.

Interaction Plot

An interaction plot displays the effect of a pair of factors on the response. For each value of one of the factors, a line connecting the mean responses at the low and high levels of the other factor is shown. An interaction effect is indicated when the lines have unequal slopes.

Lenth Plot

A Lenth plot is a bar chart used to determine possible significant effects. The plot is created using a method, proposed by Lenth (1989), that computes a simultaneous margin of error (SME) around zero. Effect sizes that exceed the SME are flagged as possibly significant.

Lenth uses a pseudostandard error (PSE) to construct the SME. A preliminary estimate of the standard error is computed as 1.5 times the median of the absolute value of the estimated effects. Then the PSE is computed based on a trimmed median of the effects. Only the effects within 2.5 times the preliminary estimate are included in the trimmed median in an attempt to include only the inactive effects in the estimate.

Levels of a Factor

Levels are the values or settings of the factors in an experiment.

Main Effect

An effect measures the extent to which the response depends on the factors involved in the effect. A main effect is the change in the response due to a single factor. For two-level factors, the main effect is the difference between the mean response at the high level of a factor and the mean response at its low level.

Main-Effects Plot

A main-effects plot displays the effect of a single factor on the response by plotting a line from the mean response at the low level of the factor to the mean response at the high level. Confidence intervals are plotted around the means. A nearly horizontal main-effect line generally indicates that the factor has little effect on the response.

A main-effects plot can be an effective way of presenting the effect of a single factor but yields little information about the whole model.

Master Model

A master model includes the effects that are initially considered for the experiment. ADX assigns a master model to each response by default. The master model is the model that is fit when you first click Fit. You can modify the master model at any time.

Minimum Aberration Design

A minimum aberration design (Fries and Hunter 1980) is designed to alias as few lower-order interactions as possible. The aberration criterion distinguishes fractional factorial designs with the same number of runs, the same number of factors, and the same resolution. Usually, you want a design with the highest resolution and the lowest aberration. All the standard fractional factorial designs in ADX are minimum aberration.

Mixed-Level Design

A mixed-level design is a relatively small design for two- and three-level factors, often used in the Taguchi (1978) approach to quality engineering. Most mixed-level designs included in the ADX Interface are orthogonal arrays. These designs usually have Resolution 3 and are ineffective for exploring interactions.

Mixture Design

The factors in a mixture design correspond to the proportion of components in a blend. They cannot be negative and must sum to one.

Refer to Cornell (1990) for details on mixture designs.

Model

The observed value for a response variable is assumed to be the sum of the effects of experimental factors, their interactions, and random error. A model is the collection of these effects together with the error structure.

In a typical study, an experiment with a model involving main effects and two-factor interactions is first run to identify significant factors. Then an experiment with a model involving the main, quadratic, and interaction effects of these significant factors is run to optimize the responses.

Normal Plot

A normal plot is constructed by plotting the sorted values of the responses (empirical quantiles) versus the theoretical quantiles from a normal distribution.

The normal plot is used to determine active (significant) effects. Inactive effects correspond to points that lie on or near a line whose slope is the standard deviation of the error, while active effects correspond to points that depart from the line.

Optimal Design

Standard designs have assured degrees of precision and orthogonality that are important for the exploratory nature of experimentation. However, when standard designs are inappropriate you can use optimal designs. You can use optimal designs under the following conditions:

when not all combinations of the factor levels are feasible
when the region of experimentation is irregularly shaped
when resource limitations restrict the number of experiments that can be performed
when there is a nonstandard model

For any of these situations you can generate an efficient experimental design by specifying a set of candidate design points and a model. ADX uses PROC OPTEX to determine points so that the terms in the model can be estimated as efficiently as possible. Refer to the SAS/QC User's Guide for details.

Orthogonal Array

The orthogonal arrays included in the ADX Interface are relatively small designs for two- and three-level factors. These are often used in the Taguchi (1978) approach to quality engineering. They are also called mixed-level designs.

Orthogonal arrays can be used for studying quantitative factors, but the requirement of orthogonality between factors usually makes the designs large, while providing insufficient information about interactions. In studying quantitative factors, it is usually more appropriate to use two-level designs, followed by response surface designs.

Outer Array

In Taguchi (1978) applications, the response observed for each combination of factors is a function, called the signal-to-noise ratio, computed over several observations (the outer array). The outer array represents a range of uncontrollable operating conditions (noise), and the intent is to estimate the effect of these conditions on the response.

Outlier

An outlier is a data point that differs from the general trend of the data by more than is expected by chance alone. An outlier might be an erroneous data point or one not explained by the same model as the rest of the data.

Pareto Plot

A Pareto plot is a bar chart of scaled absolute effect estimates. By default, the estimates are scaled by the sum of the absolute effect estimates. The plot can also display the square of the estimates scaled by the sum of squares of the estimates. In both cases, the bars are sorted in descending order.

In a typical Pareto plot, there are a few tall bars and many short bars. This illustrates the Pareto principle: in a typical experiment, relatively few effects will be significant.

Plackett-Burman Design

A Plackett-Burman design is a minimum-run, orthogonal design for estimating main effects. In ADX, Plackett-Burman designs are available for 2 to 47 factors. The number of runs in a Plackett-Burman design is the smallest multiple of 4 greater than the number of factors.

These designs estimate only main effects, and these effects are confounded with a linear combination of two-factor interaction effects. Thus, they are considered Resolution 3 designs. If analysis suggests that interaction effects are active, these designs can be augmented.

Plackett-Burman designs are primarily useful for screening a large number of factors, and should be used with caution.

Randomization

In a properly designed experiment, it is essential to randomize the order of the runs. This is done to neutralize the effect of any systematic biases that might be involved in the experiment and to validate the assumptions underlying the analysis. The ADX Interface makes it easy to randomize a design.

Regression

A regression is a function that describes the relationship between an expected response and one or more effects. The most common regression is linear regression, where the method of least squares is used to estimate the coefficients in a linear function of effects (main effects or interactions).

ADX uses regression techniques to fit a predictive model to a response.

Regression Coefficients

A linear regression model has the form

$\mathbf{e}(y)= b_0 + b_1x_1 + b_2x_2 + ... + b_px_p$

where

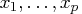are the independent variables of the model. The

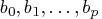terms are the regression coefficients; they show the direction and magnitude of the dependence of the expected response on the associated independent variables.

Regular Fractional Factorial Design

In regular fractional factorial designs, any two effects are either orthogonal or completely aliased. That is, for every pair of effects, either every level of one occurs with every level of the other, or every level of one occurs within exactly one level of the other. In general, a small fractional factorial design will admit fewer estimable effects, and it will involve more aliased effects than a large one. In ADX, fractional factorial designs are available for as many as 50 factors and as many as 128 runs, and in blocks with as few as two runs. Design and block sizes are always powers of 2.

Residual Plot

An important assumption in regression analysis is that the residual errors, the deviations of the observed values of the response from their expectations, are independent and identically distributed with a mean of zero. You can verify this assumption by viewing a residual plot.

Resolution

The resolution of a design gives an indication of which effects can be estimated. If a design has Resolution 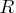, then all interactions up to order 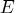are estimable and are not aliased with each other, where 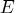is the integer part of 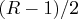. Furthermore, if 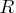is even, these interactions are not aliased with any 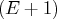-order interactions.

In particular:

In a design of Resolution 3, the main effects are not aliased with each other, but they are confounded with two-factor interactions.
In a design of Resolution 4, the main effects are not aliased with each other or with any two-factor interactions, but some two-factor interactions are aliased with each other.
In a design of Resolution 5 or more, all main effects and two-factor interactions are estimable free of each other.

Note: Roman numerals are often used to denote resolution.

Response

Designed experiments study the dependence of the response on the factors of the design. Often this involves identifying the significant factors and then optimizing the response. The experimental design consists of the specific combinations of levels of the design factors that are chosen for observation of the response.

Response Surface Design

A response surface design is often used to model both the linear and the quadratic behavior of the response over the design region. Typically, a preliminary two-level design has already been run to determine the significant factors, and now you want to study the relationship between the response and these significant factors in more detail.

Run

A run is the basic experimental unit, with one setting for each of the factors of the experiment and for which a single value will be observed for each response. In industrial applications, this might correspond to a single run of the process, with certain settings for the various process variables. Choose the number of runs in the experimental design by balancing all other design parameters---number of factors, resolution, and block size---against your experimental budget. As a general rule, you should spend about 25% of your experimental budget on a preliminary, exploratory study such as a screening experiment.

Saturated Design

In a saturated design (also called a screening experiment or an orthogonal array) there are as many observations as there are parameters to estimate in the model. Thus, there are no degrees of freedom left over to provide an independent estimate of the error variance. A saturated design allows many factors to be studied with relatively few runs, but because it gives no information about the underlying variation, it should be used cautiously.

Scatter Plot

A scatter plot is a two- or three-dimensional plot showing the joint variation of two (or three) variables from a group of observations. The coordinates of each point in the plot correspond to the data values for a single observation.

Signal-to-Noise Ratio

A signal-to-noise ratio is one of a variety of measures of response performance, relating the mean response (or "signal") to the variation in the response (or "noise"). The use of signal-to-noise ratios is associated with the Taguchi (1978) approach to quality engineering. You might want to estimate the effect of factors on the value of the response or on its variability or perhaps on both simultaneously. Alternatively, you might want a performance measure that increases as the response decreases.

Signal-to-noise ratios are calculated for groups of experimental runs, so multiple response values are required. Usually these are observed over an outer array.

Simplex-Centroid Design

A simplex-centroid design of degree 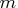is composed of mixtures consisting of the following types of blends:

only one component present
all pairs of two components present in equal amounts
all triples of three components present in equal amounts
and so on, up to all combinations of components present in equal amounts
all components present in equal amounts (the centroid)

With such a design it is possible to fit a mixture model up to degree

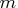A 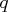-component simplex-centroid design consists of 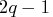distinct design points. Because they are relatively efficient designs for fitting the special cubic model, simplex-centroid designs are often used when the experimenter believes that some cubic terms might be missing in the final model. The simplex-centroid design is also used to provide experimental coverage of the response surface in the center of planes and hyperplanes.

Simplex-Lattice Design

A simplex lattice is a uniformly spaced set of points (or "lattice") on a simplex. When a simplex-lattice design is used in mixture experiments, the responses are measured at the simplex-lattice composition points.

Small Composite Design

For a small composite design, the fractional portion is neither a complete 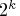nor a Resolution 5 fraction, but rather a special Resolution 3 fraction in which no four-letter word occurs among the defining relations. As a result, the total run size is reduced from that of a central composite design. Small composite designs are less efficient for estimating linear and interaction coefficients than central composite designs.

Split-Plot Design

A split-plot design modifies the classical fractional factorial design structure to accommodate differences in the precision to which different effects can be estimated. The split-plot structure was originally designed to analyze agricultural experiments in which a large area of land used for the experiment was divided into large plots, called whole plots. These whole plots were subdivided into smaller plots, called subplots, and treatments were assigned to units within the subplots. The assumption was that the subplots were more homogeneous than the whole plots and therefore analysis of effects between the subplots required a different analysis from the effects between the whole plots.

Today, the split-plot construction is used to accommodate randomization issues such as hard-to-change factors and environmental nuisance factors. ADX uses the mixed-model approach to analyzing split plots.

Surface Plot

A surface plot is a graph of one response against two factors. ADX enables you to rotate the surface for maximum utility.

Two-Level Design

In a two-level design, each factor occurs at only two levels, usually a high value and a low value. A two-level screening design is usually used at the initial stages of experimentation to identify factors that significantly affect the response.

Top of Page